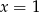/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9912121

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równania stycznych do okręgu o równaniu 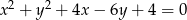2 2 x + y + 4x − 6y + 4 = 0 , równoległych do osi rzędnych układu współrzędnych.

Rozwiązanie

Przekształćmy równanie okręgu tak, aby było widać jaki ma środek i promień.

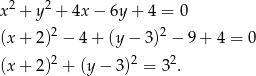
2 2 x + y + 4x − 6y+ 4 = 0 (x + 2 )2 − 4 + (y − 3)2 − 9 + 4 = 0 (x + 2 )2 + (y − 3)2 = 32.

Jest więc to okrąg o środku 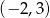(− 2,3) i promieniu 3. Możemy teraz zrobić szkicowy rysunek.

PIC

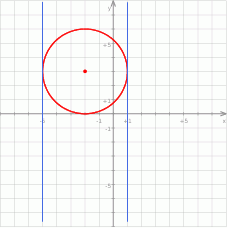
Z obrazka widać, że szukane styczne to proste 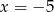x = − 5 i x = 1 .  
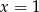Odpowiedź: 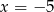x = −5 i x = 1

Wersja PDF