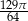/Szkoła średnia/Geometria/Geometria analityczna

Zadanie nr 9942779

Dodaj do ulubionych
Dodaj do rozwiązanych

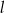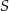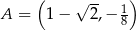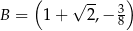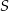Prosta l przecina okrąg o środku S w punktach ( √ -- 1) A = 1 − 2,− 8 i ( ) √ -- 3 B = 1 + 2,− 8 . Punkt S leży na prostej 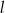l . Oblicz pole koła ograniczonego tym okręgiem.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

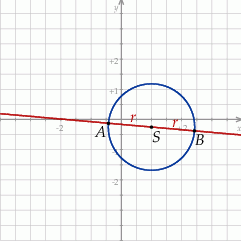
Z podanych informacji wiemy, że odcinek 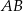AB jest średnicą danego okręgu, więc jego promień jest równy

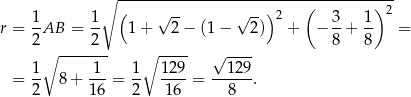
∘ -------------------------------------- 1 1 ( √ -- √ --) 2 ( 3 1) 2 r = -AB = -- 1 + 2 − (1 − 2) + − --+ -- = 2∘ ----2-- ∘ ---- ---- 8 8 1 1 1 129 √ 129 = -- 8+ ---= -- ----= ------. 2 16 2 16 8

Pole koła jest więc równe

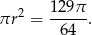
129π πr2 = -----. 64

 
Odpowiedź: 129π 64

Wersja PDF