/Szkoła średnia/Nierówności/Z pierwiastkami

Zadanie nr 3160865

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 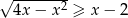√ -------2 4x − x ≥ x − 2 .

Rozwiązanie

Ponieważ

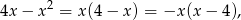
2 4x − x = x(4 − x) = −x (x− 4),

więc wyrażenie pod pierwiastkiem jest nieujemne tylko dla 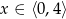x ∈ ⟨0,4⟩ . Oczywiście chciałoby się podnieść nierówność do kwadratu. Aby to zrobić musimy wiedzieć, że obie strony są nieujemne. Lewa jest. Jeżeli prawa jest ujemna, czyli dla 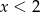x < 2 , nierówność jest oczywiście spełniona – mamy więc rozwiązanie 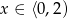x ∈ ⟨0,2 ) . Pozostało sprawdzić co się dzieje dla 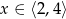x ∈ ⟨2,4⟩ . Przekształacamy

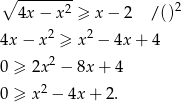
∘ -------- 2 4x − x2 ≥ x − 2 /() 2 2 4x− x ≥ x − 4x + 4 0 ≥ 2x2 − 8x + 4 2 0 ≥ x − 4x + 2.

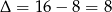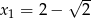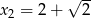Liczymy Δ = 16 − 8 = 8 , √ -- x1 = 2 − 2 , √ -- x 2 = 2+ 2 . Stąd √ -- √ -- x ∈ ⟨2 − 2,2 + 2 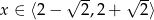⟩ . Stąd rozwiązaniem nierówności jest zbiór

√ -- ⟨0,2 + 2⟩.

 
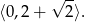
Odpowiedź: ⟨0,2 + √ 2⟩

Wersja PDF