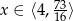/Szkoła średnia/Nierówności/Z pierwiastkami

Zadanie nr 3235956

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 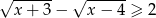√ ------ √ ------ x + 3 − x − 4 ≥ 2 .

Rozwiązanie

Ustalmy najpierw jaka jest dziedzina nierówności.

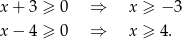
x + 3 ≥ 0 ⇒ x ≥ − 3 x − 4 ≥ 0 ⇒ x ≥ 4 .

Zatem musi być 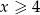x ≥ 4 .

Sposób I

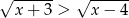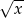Zauważmy, że √ ------ √ ------ x + 3 > x− 4 (bo √ -- x jest funkcją rosnącą), więc lewa strona jest dodatnia. Możemy zatem nierówność podnieść stronami do kwadratu.

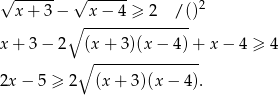
√ ------ √ ------ x + 3 − x − 4 ≥ 2 /()2 ∘ --------------- x + 3 − 2 (x + 3 )(x− 4)+ x− 4 ≥ 4 ∘ --------------- 2x − 5 ≥ 2 (x + 3)(x − 4).

Przy naszym założeniu 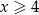x ≥ 4 lewa strona jest dodatnia, możemy więc znowu podnieść do kwadratu.

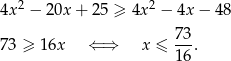
2 2 4x − 20x + 25 ≥ 4x − 4x − 4 8 73- 73 ≥ 16x ⇐ ⇒ x ≤ 16 .

W połączeniu z dziedziną daje to zbiór 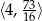⟨4, 73⟩ 16 .

Sposób II

Tym razem przenieśmy jeden z pierwiastków na prawą stronę nierówności.

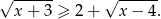
√ ------ √ ------ x + 3 ≥ 2 + x − 4.

Obie strony są nieujemne, więc podnosimy nierówność stronami do kwadratu.

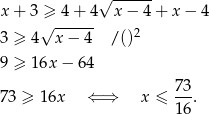
√ ------ x+ 3 ≥ 4 + 4 x − 4 + x − 4 √ ------ 3 ≥ 4 x − 4 /()2 9 ≥ 16x − 64 73 ≥ 16x ⇐ ⇒ x ≤ 7-3. 1 6

W połączeniu z dziedziną daje to zbiór 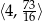⟨4, 7136⟩ .  
Odpowiedź: x ∈ ⟨4, 73-⟩ 16

Wersja PDF