/Szkoła średnia/Nierówności/Z pierwiastkami

Równania i nierówności - interpretacja geometryczna

Zacznijmy od równania postaci:

f(x) = g (x).

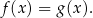
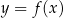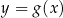O takim równaniu możemy myśleć następująco: rysujemy wykresy funkcji y = f(x) i y = g(x) w tym samym układzie współrzędnych i odczytujemy ich punkty przecięcia. Powinno być jasne, że pierwsze współrzędne tych punktów to dokładnie rozwiązania interesującego nas równania (w tych punktach wartości obu funkcji są równe). Przykłady Interpretacja geometryczna równań i nierówności bywa niezwykle użyteczna. Na ogół o wiele łatwiej jest nam myśleć o obrazkach (wykresach), niż o własnościach liczb (przekształceniach równań/nierówności).

Ile rozwiązań może mieć równanie 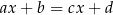ax + b = cx + d ?
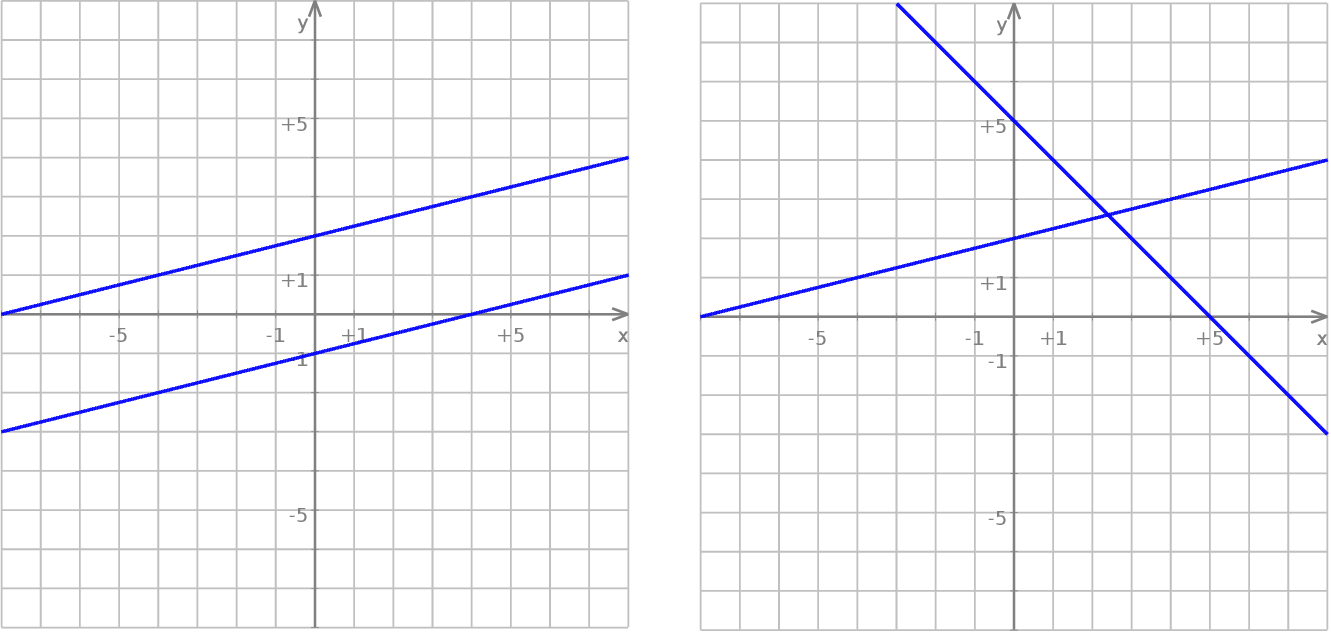
W pierwszej chwili pytanie wydaje się bez sensu, bo nic nie wiemy o parametrach 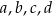a,b,c,d . Jednak wiemy jaka jest interpretacja geometryczna tego równania: wykresy obu jego stron to proste na płaszczyźnie i rozwiązania równania odpowiadają punktom wspólnym tych prostych.

ZINFO-FIGURE

Ile punktów wspólnych mogą mieć dwie proste? – mogą być rozłączne, mogą przecinać się w jednym punkcie, mogą się pokrywać. Zatem to równanie może być sprzeczne, może mieć jedno rozwiązanie, może być tożsamością (każda liczba je spełnia). Tak więc znamy dość dokładną odpowiedź, pomimo, że nic nie wiemy o liczbach 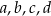a,b,c,d . W szczególności nie da się tak dobrać tych parametrów, żeby równanie miało np. dokładnie dwa rozwiązania.
Oczywiście do takich samych wniosków można dojść przekształcając równanie, ale interpretacja geometryczna daje nam poczucie, że naprawdę wiemy o co chodzi – rachunkami możemy najwyżej potwierdzić nasze przypuszczenia.

Jeżeli poprzedni przykład był zbyt prosty, to zastanówmy się ile rozwiązań może mieć równanie

ax + b = √x-.

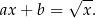
Tu już rachunki nie są takie oczywiste. Możemy jednak myśleć o wykresach. Wiemy jak wygląda wykres funkcji 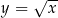√ -- y = x , jest to połowa poziomej paraboli. Wykres lewej strony to prosta.

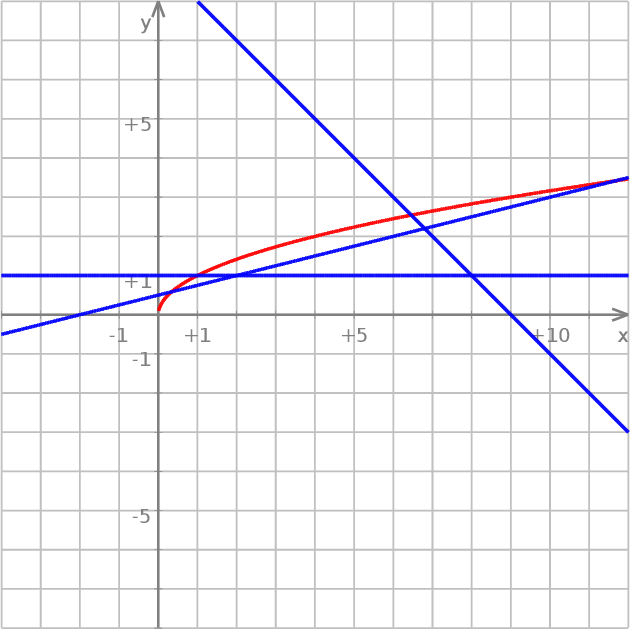
ZINFO-FIGURE

Jeżeli zaczniemy sobie szkicować różne możliwe konfiguracje to powinno być jasne, że wyjściowe równanie może mieć 0,1 lub 2 rozwiązania. Nigdy nie będzie większej liczby rozwiązań (np. 3).

Dokładne rozwiązania Po tych optymistycznych przykładach, trzeba sobie jasno powiedzieć, że nie da się nawet z najdokładniejszego wykresu odczytać dokładnego rozwiązania równania. Można natomiast (czasami) z wykresu takie rozwiązanie odgadnąć, a potem sprawdzić, że się zgadza.

Rozwiążmy graficznie równanie 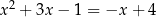x2 + 3x − 1 = −x + 4 .

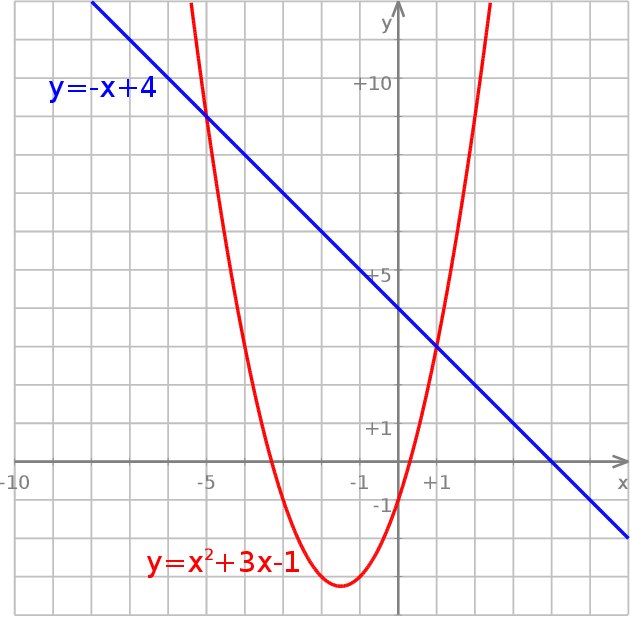
ZINFO-FIGURE

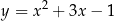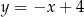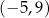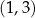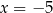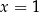Jeżeli wykonamy w miarę dokładny rysunek wykresów funkcji y = x2 + 3x− 1 oraz y = −x + 4 to widać, że przecinają się w okolicach punktów (− 5,9) i (1,3) . W takim razie sprawdzamy, czy liczby x = − 5 i x = 1 rzeczywiście są rozwiązaniami wyjściowego równania. Gdy się to zrobi, okaże się, że są.

Liczba rozwiązań O ile samo graficzne rozwiązywanie równań nie jest zbyt użyteczne, to już graficzne ustalenie ile rozwiązań ma równanie (często z parametrem) potrafi być niezwykle wygodne. Najczęściej występująca sytuacja to równania z parametrem postaci

f(x) = m.

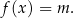
W takiej sytuacji rysujemy wykres funkcji 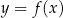y = f(x) i badamy ile ma on punktów wspólnych z poziomą prostą 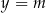y = m , w zależności od wartości parametru m .

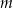Ustalmy dla jakich wartości parametru 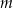m równanie 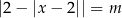|2 − |x − 2|| = m ma dokładnie cztery rozwiązania.
Szkicujemy wykres funkcji 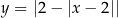y = |2 − |x− 2|| : zaczynamy od wykresu 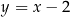y = x− 2 i część powyżej osi 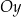Oy odbijamy do na dół (mamy 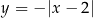y = − |x − 2| ). Potem otrzymany wykres przesuwamy o dwie jednostki do góry i odbijamy część poniżej osi Oy do góry.

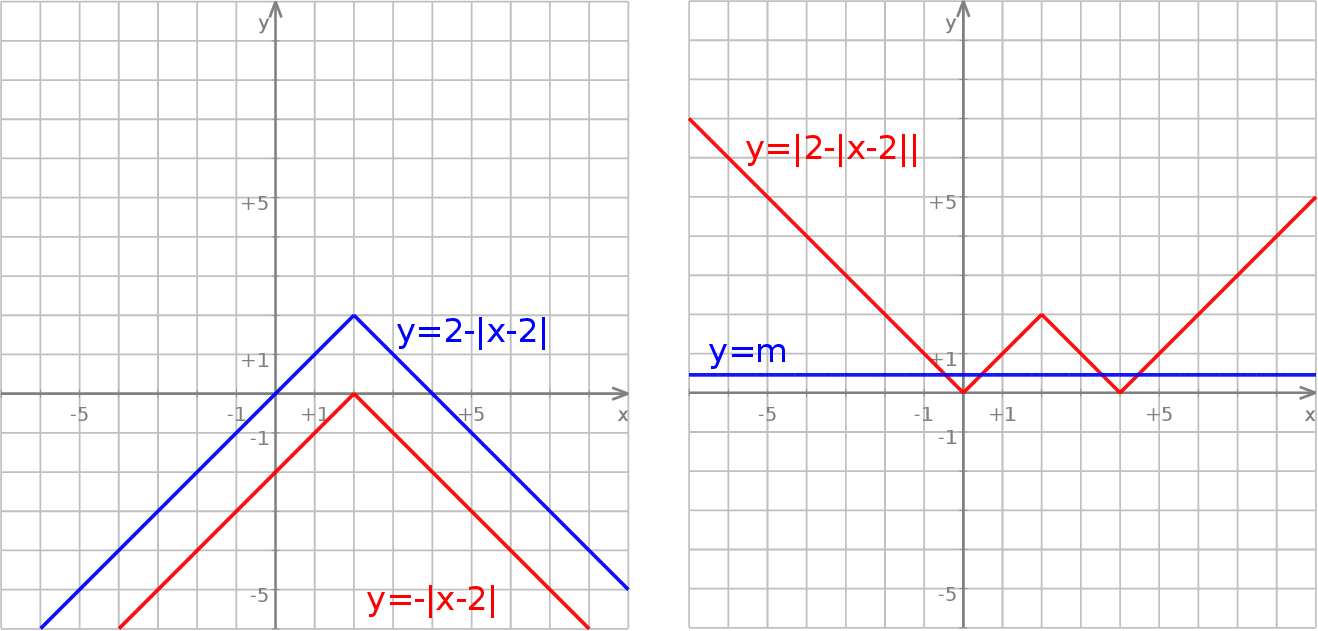
ZINFO-FIGURE

Z wykresu widać, że równanie będzie miało 4 rozwiązania dla 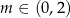m ∈ (0,2) . Oczywiście jest to bardzo elegancka metoda, dla porównania spróbujcie otrzymać tę samą odpowiedź algebraicznie.

Nierówności Wartość wykresów dramatycznie rośnie, gdy wkraczamy w świat nierówności. W przypadku typowych nierówności postaci

f(x) > g(x)

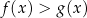
pytanie o rozwiązania to po prostu pytanie o przedziały, na których wykres funkcji 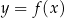y = f (x) jest powyżej wykresu funkcji 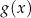g(x) . Dokładnie z tego powodu warto nauczyć się kształtów wykresów najczęściej pojawiających się funkcji.

Rozwiążmy graficznie nierówność 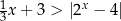13 x+ 3 > |2x − 4| .
Rysujemy wykresy obu stron nierówności.

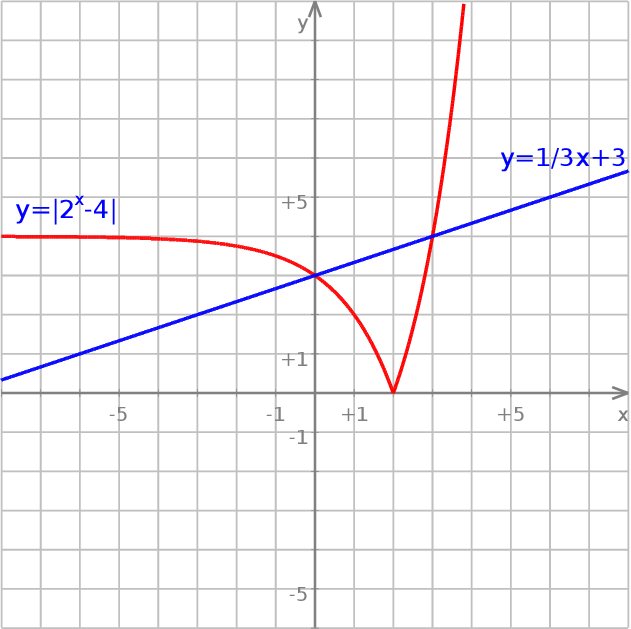
ZINFO-FIGURE

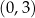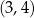Wykres lewej strony to prosta przechodząca przez punkty (0,3) i (3,4) . Prawą stronę rysujemy zaczynając od wykresu funkcji 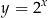y = 2x , potem przesuwamy go o 4 jednostki w dół i odbijamy część poniżej osi 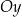Oy do góry. Z wykresu ’zgadujemy’ punkty przecięcia: 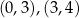(0,3),(3,4) , które sprawdzamy podstawiając do wzorów. Widać teraz, że lewa strona jest większa od prawej na przedziale (0 ,3) .

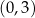Podzbiory płaszczyzny Inny popularny motyw to wyznaczanie podzbiorów płaszczyzny spełniających zadane warunki. Możliwe są tu różne konfiguracje, ale na ogół staramy się sprowadzić podane warunki do kilku równań (nierówności) postaci 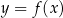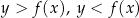y = f(x) (y > f (x), y < f(x) ). Każdy z takich warunków wyznacza na płaszczyźnie kawałek wykresu funkcji 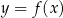y = f(x) (w przypadku nierówności obszar powyżej/poniżej wykresu funkcji y = f(x) ).

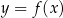Wyznaczmy zbiór punktów płaszczyzny, których współrzędne spełniają równanie 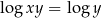lo gxy = logy .
Ze względu na prawą stronę, musi być 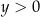y > 0 , co w połączeniu z logarytmem z lewej strony daje 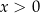x > 0 . Przy tych założeniach opuszczamy logarytmy i mamy

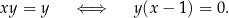
xy = y ⇐ ⇒ y(x− 1) = 0.

Ponieważ 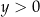y > 0 , otrzymujemy stąd x = 1 .

ZINFO-FIGURE

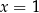Wyznaczmy wszystkie punkty 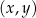(x,y) płaszczyzny, których współrzędne spełniają nierówność

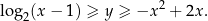
lo g (x− 1) ≥ y ≥ −x 2 + 2x . 2

Szkicujemy wykresy obu stron nierówności.

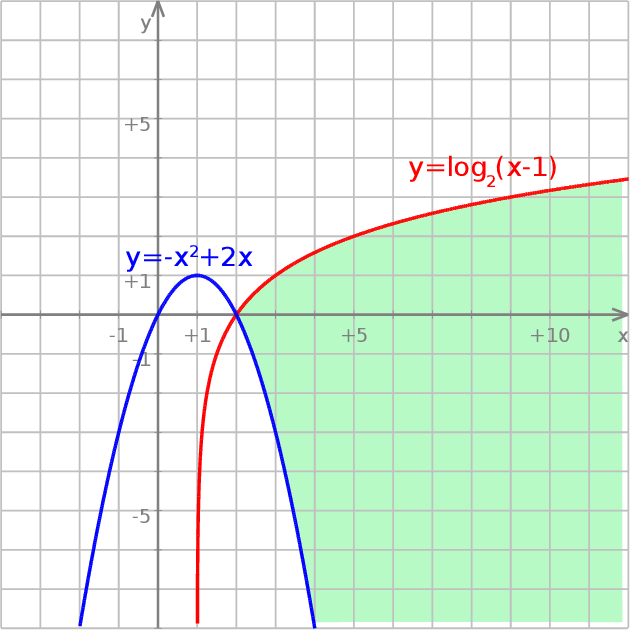
ZINFO-FIGURE

Z obrazka widzimy, że wykresy przecinają się w jednym punkcie 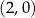(2,0) (co sprawdzamy wstawiając do wzorów!). Pozostało teraz zaznaczyć obszar zawarty między obydwoma wykresami.

Powyżej wyświetlona jest tylko pierwsza część poradnika. Druga część jest dostępna tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.