/Szkoła średnia/Równania/Z wartością bezwględną/Układy równań

Zadanie nr 7758345

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż układ równań 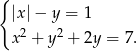{ |x |− y = 1 x2 + y2 + 2y = 7.

Rozwiązanie

Sposób I

Zacznijmy od zapisania drugiego równania tak, aby było widać jaki to jest okrąg.

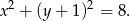
x2 + (y + 1)2 = 8.

Jest to zatem okrąg o środku 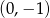(0,− 1 ) i promieniu √ -- 2 2 ≈ 2,8 .

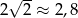Pierwsze równanie możemy natomiast napisać jako wzór funkcji

y = |x |− 1.

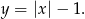
Jeżeli teraz naszkicujemy obie te krzywe w układzie współrzędnych to widać, że przecinają się w okolicach punktów 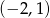(− 2,1) i (2,1) .

PIC

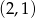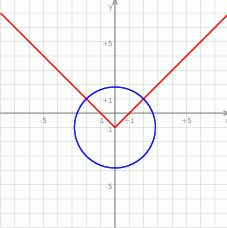
Aby sprawdzić, czy istotnie są to punkty przecięcia, podstawiamy ich współrzędne do obu równań. Łatwo sprawdzić, że wszystko się zgadza.

Sposób II

Możemy też układ rozwiązać algebraicznie. Podstawiamy 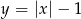y = |x|− 1 do drugiego równania.

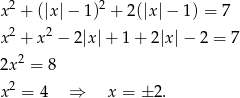
x2 + (|x |− 1)2 + 2(|x|− 1) = 7 2 2 x + x − 2|x |+ 1 + 2|x|− 2 = 7 2x2 = 8 x2 = 4 ⇒ x = ± 2.

Stąd 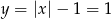y = |x|− 1 = 1 .  
Odpowiedź: 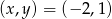(x,y) = (− 2,1) lub (x ,y ) = (2,1)

Wersja PDF