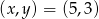Zadanie nr 9343991
Rozwiąż algebraicznie układ równań 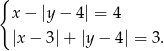
Rozwiązanie
Dodajmy podane równania stronami (żeby skrócić 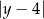 ).
).
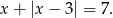
Jeżeli 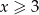 to mamy
to mamy
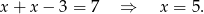
Jeżeli natomiast 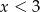 to mamy równanie
to mamy równanie
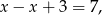
które jest sprzeczne.
Zatem 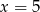 i z pierwszego równania mamy
i z pierwszego równania mamy
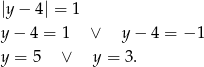
Odpowiedź: 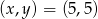 lub
lub