/Szkoła średnia/Ciągi/Arytmetyczny/W geometrii

Zadanie nr 3093600

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta prostokątnego tworzą ciąg arytmetyczny. Jedna z przyprostokątnych ma długość 6. Jaką długość ma druga przyprostokątna oraz przeciwprostokątna?

Rozwiązanie

Oznaczmy boki trójkąta przez 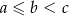a ≤ b < c . Z twierdzenia Pitagorasa mamy

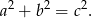
a2 + b2 = c2.

Ponadto, ponieważ liczby te tworzą ciąg arytmetyczny, mamy 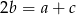2b = a+ c . Podstawiając 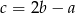c = 2b − a w powyższej równości, mamy

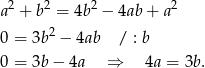
a2 + b2 = 4b2 − 4ab + a2 2 0 = 3b − 4ab / : b 0 = 3b − 4a ⇒ 4a = 3b.

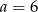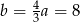Mamy teraz dwie możliwości. Jeżeli a = 6 to b = 4 a = 8 3 i

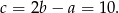
c = 2b − a = 10 .

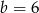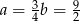Jeżeli natomiast b = 6 , to a = 3b = 9 4 2 i

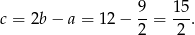
c = 2b− a = 12 − 9-= 15-. 2 2

 
Odpowiedź: 8 i 10, lub 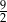9 2 i 15 2

Wersja PDF