/Szkoła średnia/Ciągi/Arytmetyczny/W geometrii

Zadanie nr 4139316

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości boków trójkąta prostokątnego o obwodzie 30 cm są pierwszym, piętnastym i siedemnastym wyrazem rosnącego ciągu arytmetycznego. Oblicz pole tego trójkąta.

Rozwiązanie

Oznaczmy długości boków trójkąta przez 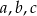a,b,c .

PIC

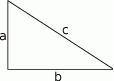
Ponieważ wiemy, że długości boków tworzą rosnący ciąg arytmetyczny, pierwszym wyrazem ciągu musi być jedna z przyprostokątnych, powiedzmy, że jest to a .

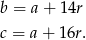
b = a + 14r c = a + 16r.

Z podanego obwodu mamy

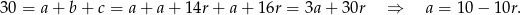
3 0 = a+ b+ c = a+ a+ 14r+ a+ 16r = 3a + 30r ⇒ a = 10− 10r.

Zatem boki trójkąta są równe

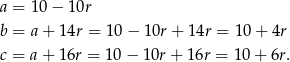
a = 1 0− 1 0r b = a + 14r = 10− 10r+ 14r = 10 + 4r c = a + 16r = 10− 10r+ 16r = 10 + 6r.

Aby wyliczyć r potrzebujemy jeszcze jednego równania – otrzymamy je z twierdzenia Pitagorasa.

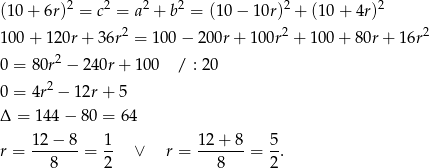
2 2 2 2 2 2 (10+ 6r) = c = a + b = (10 − 10r) + (10 + 4r) 100+ 120r + 36r2 = 1 00− 200r+ 100r2 + 100 + 80r + 16r2 2 0 = 80r − 240r + 100 / : 20 0 = 4r2 − 12r+ 5 Δ = 1 44− 80 = 64 12 − 8 1 12+ 8 5 r = -------= -- ∨ r = -------= -. 8 2 8 2

Drugie rozwiązanie daje nam 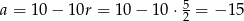a = 1 0− 10r = 10 − 10 ⋅ 52 = − 1 5 , więc je odrzucamy. Zatem 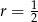r = 1 2 i wtedy 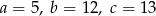a = 5 , b = 1 2, c = 13 . Zatem pole jest równe

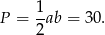
1- P = 2ab = 3 0.

 
Odpowiedź: 30 cm 2

Wersja PDF