Zadanie nr 5369555
Miary kątów wielokąta tworzą ciąg arytmetyczny, którego różnica jest równa 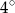 . Największy kąt ma miarę
. Największy kąt ma miarę 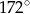 .
.
- Ile boków ma ten wielokąt?
- Ile ma przekątnych?
Rozwiązanie
- Jeżeli wielokąt ma
 boków, to suma jego kątów wynosi
boków, to suma jego kątów wynosi 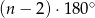 (bo przekątne wychodzące z jednego wierzchołka dzielą go na
(bo przekątne wychodzące z jednego wierzchołka dzielą go na 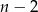 trójkątów). Mamy zatem ciąg arytmetyczny o różnicy 4, ostatnim wyrazie
trójkątów). Mamy zatem ciąg arytmetyczny o różnicy 4, ostatnim wyrazie 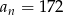 i sumie
i sumie 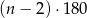 . Ponieważ
. Ponieważ 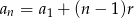 , to
, to 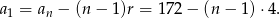
Korzystamy teraz ze wzoru na sumę wyrazów ciągu arytmetycznego
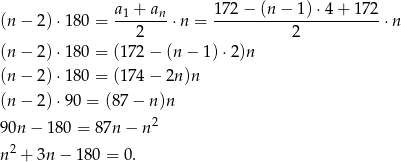
Liczymy dalej
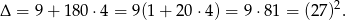
Stąd dodatni pierwiastek to
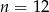 .
.
Odpowiedź: 12 boków - Każda przekątna wielokąta jest wyznaczona przez dwa wierzchołki, więc w pierwszej chwili może się wydawać, że wielokąt o
 bokach ma
bokach ma 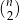 przekątnych. To jest prawie dobrze, trzeba tylko odjąć
przekątnych. To jest prawie dobrze, trzeba tylko odjąć  boków, których nie uważamy za przekątne. Przekątnych jest zatem
boków, których nie uważamy za przekątne. Przekątnych jest zatem 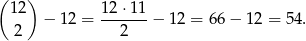
Odpowiedź: 54 przekątne

