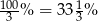Zadanie nr 8547137
Długości boków trójkąta  ,
, 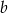 ,
,  (w podanej kolejności) tworzą ciąg arytmetyczny. Wyraź w procentach jaką część wysokości trójkąta poprowadzonej na bok długości
(w podanej kolejności) tworzą ciąg arytmetyczny. Wyraź w procentach jaką część wysokości trójkąta poprowadzonej na bok długości 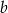 stanowi promień okręgu wpisanego w ten trójkąt.
stanowi promień okręgu wpisanego w ten trójkąt.
Rozwiązanie
Fakt, że długości boków tworzą ciąg arytmetyczny oznacza, że 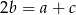 . Aby związać ze sobą wysokość
. Aby związać ze sobą wysokość 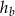 i promień
i promień  okręgu wpisanego, skorzystamy z dwóch wzorów na pole trójkąta
okręgu wpisanego, skorzystamy z dwóch wzorów na pole trójkąta
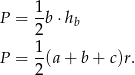
Porównujemy te dwa wzory i korzystamy z tego, że 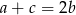 .
.
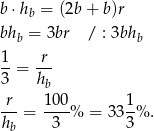
Odpowiedź: