/Szkoła średnia/Ciągi/Geometryczny/Na dowodzenie

Zadanie nr 2720720

Wykaż, że jeżeli ciąg 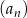(an) jest ciągiem geometrycznym, to

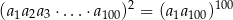
2 100 (a1a2a3 ⋅ ...⋅a100) = (a1a100)
Wersja PDF

Rozwiązanie

Korzystamy ze wzoru 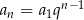n−1 an = a 1q na n –ty wyraz ciągu geometrycznego. Obliczamy najpierw wartość lewej strony równości, którą mamy udowodnić.

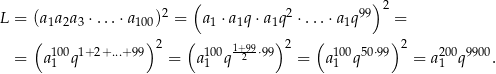
( ) 2 L = (a1a 2a 3 ⋅...⋅a100)2 = a1 ⋅a1q ⋅a1q2 ⋅...⋅a1q99 = ( ) ( ) ( ) 100 1+2+...+99 2 100 1+299⋅99 2 100 50⋅99 2 200 9900 = a1 q = a1 q = a1 q = a1 q .

Po drodze skorzystaliśmy ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego. Teraz obliczamy prawą stronę

( )100 ( )100 P = (a1a100)100 = a1 ⋅a1q99 = a21q99 = a2100q9900 = L .
Wersja PDF