/Szkoła średnia/Ciągi/Geometryczny/Na dowodzenie

Zadanie nr 4378109

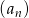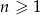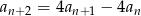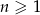Ciąg geometryczny (an ) , gdzie n ≥ 1 spełnia warunek an+2 = 4an +1 − 4an dla n ≥ 1 . Uzasadnij, że ciąg ten spełnia też warunek 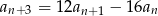an+ 3 = 12an+ 1 − 16an dla n ≥ 1 .

Wersja PDF

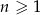Rozwiązanie

Sposób I

Aby obliczyć 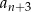an+3 podstawiamy w pierwszym z podanych warunków 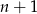n + 1 zamiast n .

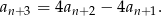
an+3 = 4an +2 − 4an+ 1.

Teraz jeszcze raz korzystamy z pierwszego warunku i podstawiamy za an+ 2 .

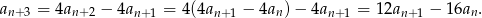
an+3 = 4an+2 − 4an+ 1 = 4(4an+ 1 − 4an )− 4an+1 = 12an +1 − 16an.

Sposób II

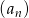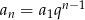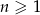Skoro ciąg (an) jest geometryczny to n−1 an = a1q dla n ≥ 1 . Korzystamy z tego wzoru w pierwszym z podanych warunków.

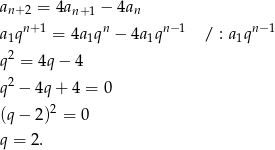
a = 4a − 4a n+ 2 n+1 n a1qn+ 1 = 4a1qn − 4a1qn− 1 / : a1qn− 1 2 q = 4q − 4 q2 − 4q + 4 = 0 (q − 2)2 = 0 q = 2.

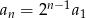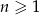To oznacza, że n−1 an = 2 a1 dla n ≥ 1 . Pozostało sprawdzić, że ciąg ten spełnia drugi z podanych warunków.

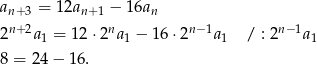
an+ 3 = 12an+ 1 − 1 6an 2n+ 2a1 = 12 ⋅2na1 − 16 ⋅2n−1a 1 / : 2n− 1a1 8 = 24− 16.

Otrzymana równość jest oczywiście spełniona, co kończy dowód.

Wersja PDF