/Szkoła średnia/Ciągi/Geometryczny/Na dowodzenie

Zadanie nr 4725038

Ciąg 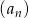(an) jest ciągiem geometrycznym. Wykaz, że ciąg 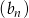(bn) określony wzorem 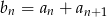bn = an + an +1 jest również ciągiem geometrycznym.

Wersja PDF

Rozwiązanie

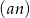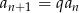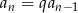Ponieważ (an) jest ciągiem geometrycznym, mamy an+1 = qan i an = qan− 1 dla pewnego 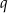q . To oznacza, że

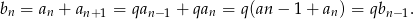
bn = an + an+ 1 = qan−1 + qan = q(an − 1+ an) = qbn− 1.

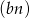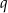To oznacza, że ciąg (bn) jest również ciągiem geometrycznym o ilorazie q .

Wersja PDF