Zadanie nr 5599569
Wykaż, że dla każdej liczby naturalnej  , liczby
, liczby 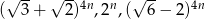 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Rozwiązanie
Musimy uzasadnić, że kwadrat środkowej liczby jest iloczynem liczb sąsiednich. Liczymy
![√ -- √ -- √ -- [ √ -- √ -- √ -- ]4n ( 3 + 2)4n ⋅( 6− 2)4n = ( 3 + 2)( 6 − 2) = ( ) ( ) √ --- √ -- √ --- √ -- 4n √ -- √ -- √ -- √ --4n = 18− 2 3 + 12 − 2 2 = 3 2 − 2 3+ 2 3− 2 2 = √ --4n 2n n 2 = ( 2) = 2 = (2 ) ,](https://img.zadania.info/zad/5599569/HzadR0x.gif)
co kończy uzasadnienie.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla każdej liczby naturalnej  , liczby
, liczby 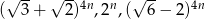 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Musimy uzasadnić, że kwadrat środkowej liczby jest iloczynem liczb sąsiednich. Liczymy
![√ -- √ -- √ -- [ √ -- √ -- √ -- ]4n ( 3 + 2)4n ⋅( 6− 2)4n = ( 3 + 2)( 6 − 2) = ( ) ( ) √ --- √ -- √ --- √ -- 4n √ -- √ -- √ -- √ --4n = 18− 2 3 + 12 − 2 2 = 3 2 − 2 3+ 2 3− 2 2 = √ --4n 2n n 2 = ( 2) = 2 = (2 ) ,](https://img.zadania.info/zad/5599569/HzadR0x.gif)
co kończy uzasadnienie.
