/Szkoła średnia/Ciągi/Geometryczny/Na dowodzenie

Zadanie nr 7624044

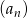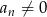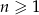Wyrazy ciągu geometrycznego (an) , w którym an ⁄= 0 dla n ≥ 1 spełniają warunek

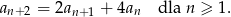
an+ 2 = 2an+1 + 4an dla n ≥ 1.

Wykaż, że wyrazy tego ciągu spełniają również warunek

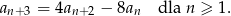
an+ 3 = 4an+2 − 8an dla n ≥ 1.
Wersja PDF

Rozwiązanie

Sposób I

Skoro 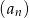(an) jest ciągiem geometrycznym to 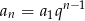n− 1 an = a1q , gdzie q jest jest ilorazem ciągu. Dany warunek przybiera więc postać

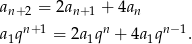
an+2 = 2an+1 + 4an a qn+1 = 2a qn + 4a qn− 1. 1 1 1

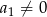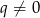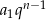Zauważmy teraz, że z założenia a1 ⁄= 0 i q ⁄= 0 , więc możemy podzielić powyższą równość stronami przez n−1 a1q .

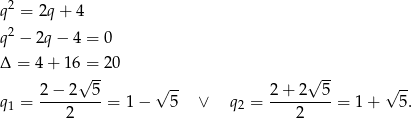
2 q = 2q + 4 q2 − 2q− 4 = 0 Δ = 4+ 16 =-20 -- 2 − 2√ 5 √ -- 2+ 2√ 5 √ -- q1 = ---------= 1 − 5 ∨ q2 = ---------= 1 + 5 . 2 2

Podobnie przekształćmy teraz warunek, który mamy wykazać.

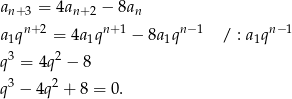
a = 4a − 8an n+3 n+2 a1qn+ 2 = 4a1qn+1 − 8a1qn− 1 / : a 1qn−1 3 2 q = 4q − 8 q3 − 4q2 + 8 = 0.

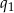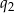Wystarczy teraz sprawdzić, że obliczone wcześniej wartości q1 i q2 spełniają ten warunek. Sprawdzamy najpierw √ -- q1 = 1 − 5 .

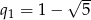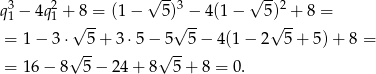
3 2 √ -- 3 √ --2 q1 − 4q1 +√8-= (1 − 5 )√ −-4(1 − 5√)-+ 8 = = 1 − 3 ⋅ 5 + 3 ⋅5− 5 5 − 4(1 − 2 5 + 5) + 8 = √ -- √ -- = 1 6− 8 5− 24+ 8 5+ 8 = 0.

Tak samo sprawdzamy 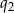q2 .

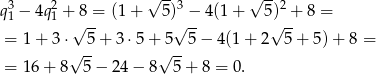
√ -- √ -- q31 − 4q21 + 8 = (1 + 5 )3 − 4(1 + 5 )2 + 8 = √ -- √ -- √ -- = 1 + 3 ⋅ 5 + 3 ⋅5+ 5 5 − 4(1 + 2 5 + 5) + 8 = √ -- √ -- = 1 6+ 8 5− 24− 8 5+ 8 = 0.

Sposób II

Tak jak w poprzednim sposobie sprawdzamy, że dany warunek jest równoważny równości

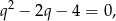
q2 − 2q − 4 = 0,

a warunek, który mamy wykazać równości

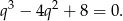
3 2 q − 4q + 8 = 0.

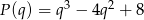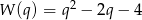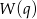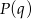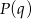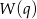Wystarczy teraz wykazać, że wielomian 3 2 P(q) = q − 4q + 8 dzieli się przez trójmian W (q) = q2 − 2q− 4 (bo wtedy każdy pierwiastek W (q) jest też pierwiastkiem P (q) ). Dzielimy P(q) przez W (q) – my zrobimy to grupując wyrazy.

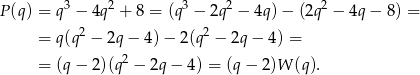
P (q) = q3 − 4q2 + 8 = (q3 − 2q2 − 4q) − (2q2 − 4q − 8) = 2 2 = q(q − 2q − 4) − 2(q − 2q − 4) = 2 = (q− 2)(q − 2q − 4) = (q − 2)W (q ).

Sposób III

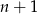Jeżeli zamienimy w danym warunku n na n + 1 otrzymamy

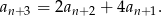
an+3 = 2an +2 + 4a . n+ 1

Teraz w tym warunku chcemy się pozbyć 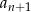a n+ 1 . Możemy to zrobić korzystając z danego warunku zapisanego w postaci 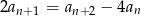2an +1 = an+ 2 − 4an . Mamy zatem

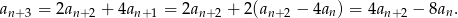
an+3 = 2an +2 + 4an+1 = 2an+2 + 2(an+ 2 − 4an ) = 4an+ 2 − 8an .

Zauważmy, że w tym sposobie nie korzystaliśmy z faktu, że 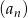(an) jest ciągiem geometrycznym!

Wersja PDF