/Szkoła średnia/Ciągi/Dowolny/Kwadratowy

Zadanie nr 1091721

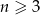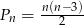Liczba przekątnych wielokąta wypukłego, w którym jest n boków i n ≥ 3 wyraża się wzorem Pn = n(n−3) 2 .

  • Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
  • Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
  • Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
  • Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
Wersja PDF

Rozwiązanie

  • Podstawiamy 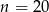n = 20 do danego wzoru.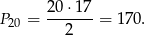
    20 ⋅17 P20 = -------= 170. 2

     
    Odpowiedź: 170

  • Musimy rozwiązać równanie
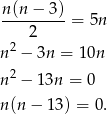
    n (n − 3) --------- = 5n 2 n 2 − 3n = 10n 2 n − 13n = 0 n (n− 13) = 0.

    Zatem n = 13 .  
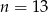    Odpowiedź: W trzynastokącie

  • Liczymy ile przekątnych mają kolejne wielokąty o parzystej liczbie boków, 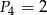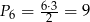P = 2 4 , P = 6⋅3-= 9 6 2 . No i możemy dalej nie liczyć, sześciokąt ma 9 przekątnych.

    Mogliśmy też wstawić do wzoru na ilość przekątnych 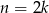n = 2k , co daje 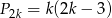P = k(2k − 3) 2k . Widać teraz, że jeżeli 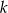k jest nieparzyste to 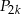P2k też jest nieparzyste. Aby mieć przykład wystarczy wziąć 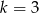k = 3 (czyli n = 6 ).  
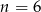    Odpowiedź: Podane zdanie nie jest prawdziwe.

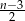  • Jeżeli n jest liczbą nieparzystą, to liczba n−3- 2 jest liczbą całkowitą i liczba przekątnych wynosi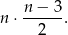
    n ⋅ n-−-3-. 2

    Widać więc, że jest ona wielokrotnością n .

Wersja PDF