/Szkoła średnia/Ciągi/Dowolny/Kwadratowy

Zadanie nr 1624957

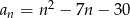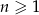Ile wyrazów ciągu o wyrazie ogólnym 2 an = n − 7n − 30 , dla n ≥ 1 , jest liczbami ujemnymi?

Wersja PDF

Rozwiązanie

Musimy rozwiązać nierówność

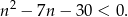
2 n − 7n − 30 < 0.

Jest to zwykła nierówność kwadratowa. Liczmy

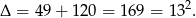
2 Δ = 49 + 1 20 = 169 = 13 .

Mamy zatem dwa miejsca zerowe

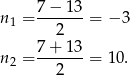
7 − 13 n1 = -------= − 3 2 n2 = 7-+-13-= 10. 2

Rozwiązaniem tej nierówności są więc liczby 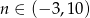n ∈ (− 3,10) , czyli pierwsze 9 wyrazów ciągu to liczby ujemne.  
Odpowiedź: 9 wyrazów

Wersja PDF