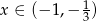Zadanie nr 9899084
Funkcje 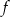 i
i 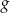 dane są wzorami
dane są wzorami 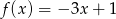 ,
, 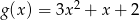 . Wyznacz zbiór argumentów
. Wyznacz zbiór argumentów  , dla których funkcja
, dla których funkcja 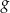 przyjmuje wartości mniejsze od funkcji
przyjmuje wartości mniejsze od funkcji 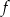 .
.
Rozwiązanie
Mamy do rozwiązania nierówność
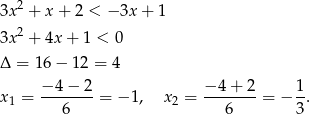
Rozwiązaniem tej nierówności jest więc przedział 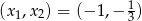 .
.
Odpowiedź: