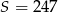/Szkoła średnia/Ciągi/Arytmetyczny/Dany wzorem

Zadanie nr 7347848

Dodaj do ulubionych
Dodaj do rozwiązanych

Ciąg arytmetyczny 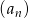(an) jest określony wzorem 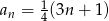1 an = 4(3n + 1) dla n ≥ 1 .

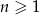  • Sprawdź, którym wyrazem ciągu 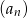(an) jest liczba 3 73 4 .
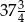  • Wśród pięćdziesięciu początkowych wyrazów ciągu 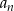a n są wyrazy będące liczbami całkowitymi. Oblicz sumę wszystkich tych wyrazów.

Rozwiązanie

  • Musimy rozwiązać równanie
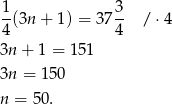
    1(3n + 1) = 373- / ⋅4 4 4 3n + 1 = 1 51 3n = 1 50 n = 50 .

     
    Odpowiedź: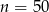 n = 50

  • Żeby zobaczyć o co chodzi, najlepiej wypisać kilka początkowych wyrazów ciągu:
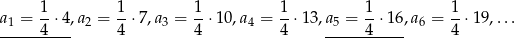
    a1 = 1-⋅4,a2 = 1-⋅7,a 3 = 1-⋅10,a4 = 1⋅ 13,a5 = 1-⋅16 ,a 6 = 1-⋅19,... ------4--- 4 4 4 -----4----- 4

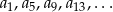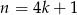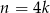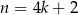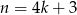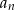Jak się wypisze jeszcze trochę to jest jasne, że wyrazy całkowite, to a1,a5,a9,a13,... , czyli te dla których n = 4k + 1 (nie będziemy tego robić, ale gdyby ktoś chciał uzasadnić tę naszą obserwację, to trzeba sprawdzić, że dla liczb postaci n = 4k , n = 4k+ 2 i n = 4k + 3 , an nie wychodzi całkowite – sprawdzenie tego jest dość proste). Musimy zatem obliczyć sumę

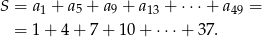
S = a + a + a + a + ⋅⋅⋅+ a = 1 5 9 13 49 = 1 + 4 + 7 + 10 + ⋅⋅ ⋅+ 37.

Ponieważ jest to suma wyrazów ciągu arytmetycznego (o różnicy 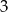3 ), to

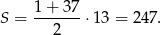
1+--37- S = 2 ⋅ 13 = 247 .

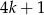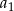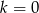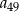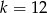Skąd wzięliśmy liczbę wyrazów? Jak mówiliśmy, indeksy wyrazów są postaci 4k + 1 oraz pierwszy (czyli a1 ) jest dla k = 0 , a ostatni (a49 ) dla k = 12 . Jest ich zatem 13 .  
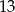Odpowiedź: S = 247

Wersja PDF