/Szkoła średnia/Ciągi/Geometryczny/Dany przez sumy wyrazów

Zadanie nr 5088584

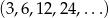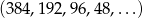Dane są dwa skończone ciągi geometryczne (3,6,12,24 ,...) i (384,1 92,96,48,...) o tej samej liczbie wyrazów. Znajdź liczbę wyrazów każdego z tych ciągów wiedząc, że łączna suma ich wyrazów wynosi 1530.

Wersja PDF

Rozwiązanie

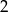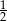Ilorazy podanych ciągów to odpowiednio 2 i 1 2 , zatem ze wzoru na sumę początkowych wyrazów ciągu geometrycznego mamy równanie

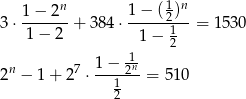
n 1 n 3 ⋅ 1-−-2-+ 38 4⋅ 1−-(-2)--= 15 30 1− 2 1 − 1 2 n 7 1-−-21n- 2 − 1 + 2 ⋅ 1 = 510 2

Podstawiając 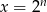x = 2n mamy równanie

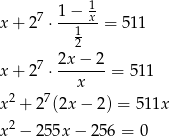
7 1-−-x1 x + 2 ⋅ 1 = 511 2 7 2x-−--2 x + 2 ⋅ x = 511 2 7 x + 2 (2x − 2) = 511x x 2 − 25 5x− 256 = 0

Gołym okiem widać, że 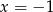x = − 1 jest pierwiastkiem, zatem na mocy wzorów Viète’a drugim pierwiastkiem jest 256. Mamy zatem

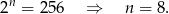
n 2 = 256 ⇒ n = 8.

 
Odpowiedź: Osiem wyrazów.

Wersja PDF