Zadanie nr 9057859

Wiedząc, że dla sum częściowych pewnego ciągu geometrycznego o wyrazach dodatnich prawdziwa jest równość 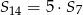S14 = 5 ⋅S7 , oblicz iloraz tego ciągu.

Rozwiązanie

Oznaczmy przez 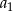pierwszy wyraz ciągu, a przez 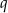jego iloraz.

Sposób I

Rozważmy najpierw przypadek, gdy 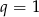q = 1 . Wtedy mamy równość

14a = 5 ⋅7a ⇒ a = 0. 1 1 1

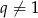Zatem q ⁄= 1 (bo ciąg mam mieć wyrazy dodatnie). Korzystając ze wzoru sumę częściową ciągu geometrycznego, podaną równość możemy zapisać w postaci

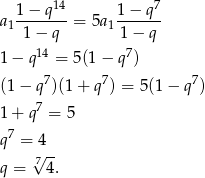
14 7 a 1-−-q-- = 5a 1−--q-- 1 1 − q 11 − q 14 7 1− q = 5(1 − q ) (1− q7)(1+ q7) = 5(1 − q7) 7 1+ q = 5 q7 = 4 √ -- q = 74.

Sposób II

Napiszmy podaną równość

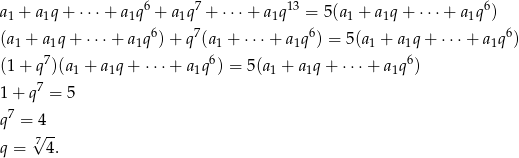
a 1 + a1q + ⋅⋅⋅ + a1q6 + a1q7 + ⋅⋅⋅+ a1q13 = 5(a1 + a1q+ ⋅⋅⋅+ a1q 6) 6 7 6 6 (a 1 + a1q + ⋅⋅⋅ + a1q )+ q (a1 + ⋅⋅⋅+ a 1q ) = 5(a1 + a1q+ ⋅⋅⋅+ a 1q ) (1 + q7)(a + a q + ⋅⋅⋅ + a q6) = 5(a + a q + ⋅⋅⋅ + a q6) 1 1 1 1 1 1 1 + q7 = 5 7 q = √4-- q = 7 4.

Odpowiedź: √ -- 74