/Szkoła średnia/Ciągi/Geometryczny/Dany przez sumy wyrazów

Zadanie nr 9196071

Dodaj do ulubionych
Dodaj do rozwiązanych

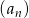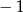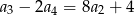Pierwszy wyraz nieskończonego ciągu geometrycznego (an) jest równy − 1 . Wyraz drugi, trzeci i czwarty spełniają warunek a3 − 2a 4 = 8a2 + 4 .

  • Oblicz iloraz ciągu (a ) n .
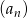  • Określ, czy ciąg 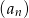(an) jest rosnący, czy malejący.

Rozwiązanie

  • Liczymy
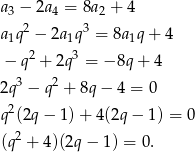
    a3 − 2a4 = 8a 2 + 4 2 3 a1q − 2a1q = 8a1q+ 4 − q2 + 2q3 = − 8q + 4 3 2 2q − q + 8q − 4 = 0 q2(2q − 1) + 4(2q − 1 ) = 0 (q2 + 4)(2q − 1) = 0.

    Ponieważ 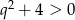2 q + 4 > 0 , więc jedynym pierwiastkiem tego równania jest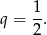

    1- q = 2.

     
    Odpowiedź: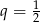 1 q = 2

  • Zapiszmy wzór na n -ty wyraz ciągu (an)
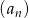
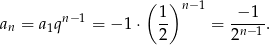
    ( ) n−1 1 n−1 − 1 an = a 1q = − 1 ⋅ 2- = -n−1. 2

    Jest to rosnący ciąg geometryczny (wraz ze wzrostem n wyrazy ciągu są coraz bliższe 0). Łatwo to sprawdzić licząc różnicę kolejnych wyrazów.

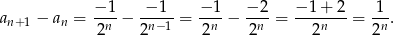
    an+1 − an = −-1-− −-1--= −-1-− −-2-= −-1+--2 = 1-. 2n 2n−1 2n 2n 2n 2n

    Różnica wyszła dodatnia, więc ciąg jest rosnący.  
    Odpowiedź: Ciąg jest rosnący

Wersja PDF