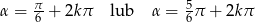Zadanie nr 4802711
Wyznacz wszystkie wartości  , gdzie
, gdzie 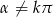 ,
, 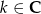 , dla których trzy liczby
, dla których trzy liczby 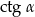 ,
, 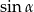 ,
, 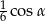 , tworzą ciąg geometryczny (w podanej kolejności).
, tworzą ciąg geometryczny (w podanej kolejności).
Rozwiązanie
Trzy niezerowe liczby 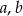 i
i  tworzą ciąg geometryczny wtedy i tylko wtedy gdy
tworzą ciąg geometryczny wtedy i tylko wtedy gdy 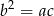 . Mamy zatem równanie
. Mamy zatem równanie
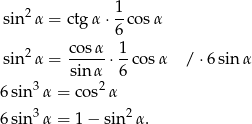
Podstawiamy teraz 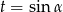 i otrzymujemy równanie wielomianowe
i otrzymujemy równanie wielomianowe
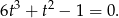
Jak zwykle szukamy pierwiastków wymiernych tego równania. Szukamy wśród liczb postaci 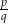 , gdzie
, gdzie 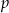 dzieli -1, a
dzieli -1, a 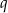 dzieli 6. Szukamy zatem wśród liczb
dzieli 6. Szukamy zatem wśród liczb
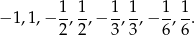
Jak zaczniemy to sprawdzać, to okaże się, że 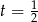 jest pierwiastkiem. Dzielimy teraz dany wielomian przez
jest pierwiastkiem. Dzielimy teraz dany wielomian przez 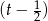 . My, jak zwykle, zrobimy to grupując wyrazy.
. My, jak zwykle, zrobimy to grupując wyrazy.
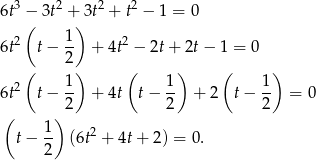
Ponieważ wielomian kwadratowy w nawiasie nie ma pierwisatków (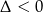 ),
), 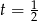 jest jedynym rozwiązaniem. Mamy zatem
jest jedynym rozwiązaniem. Mamy zatem 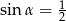 , czyli
, czyli
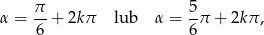
gdzie 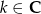 .
.
Odpowiedź: