/Szkoła średnia/Ciągi/Geometryczny/Trzywyrazowy/1 niewiadoma

Zadanie nr 6609067

Dodaj do ulubionych
Dodaj do rozwiązanych

Wiadomo, że liczby 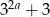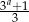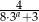2a 3 + 3 , 3a+1 3 , --4--- 8⋅3a+3 są odpowiednio pierwszym, drugim i trzecim wyrazem nieskończonego ciągu geometrycznego. Wyznacz a . Dla wyznaczonej wartości a zapisz wzór tego ciągu i oblicz sumę jego wszystkich wyrazów.

Rozwiązanie

Liczby niezerowe 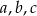a,b,c są trzema kolejnymi wyrazami ciągu geometrycznego jeżeli 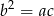b2 = ac . Mamy zatem

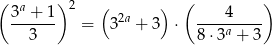
( a ) 2 ( ) ( ) 3-+--1- 2a ----4---- 3 = 3 + 3 ⋅ 8 ⋅3a + 3

Aby uprościć sobie trochę przekształcanie powyższego równania oznaczmy 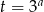t = 3a .

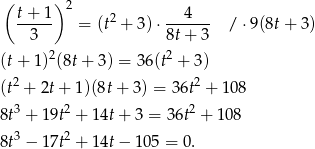
( t+ 1 )2 4 ----- = (t2 + 3) ⋅------ /⋅ 9(8t+ 3 ) 3 8t+ 3 (t + 1)2(8t+ 3) = 36(t2 + 3) (t2 + 2t+ 1)(8t+ 3) = 36t2 + 108 3 2 2 8t + 19t + 14t+ 3 = 36t + 108 8t3 − 17t2 + 14t− 105 = 0 .

Szukamy teraz pierwiastków całkowitych tego równania – sprawdzamy najpierw dzielniki wyrazu wolnego 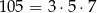105 = 3 ⋅5 ⋅7 . Jednym z pierwiastków jest 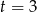t = 3 , więc dzielimy ten wielomian przez 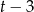t− 3 . My jak zwykle zrobimy to grupując wyrazy.

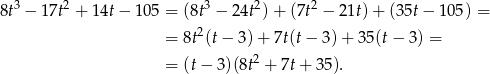
3 2 3 2 2 8t − 17t + 14t − 105 = (8t − 24t ) + (7t − 21t)+ (35t− 105) = = 8t2(t − 3) + 7t(t− 3)+ 3 5(t− 3) = = (t− 3)(8t2 + 7t+ 35).

Trójmian w nawiasie nie ma rozwiązań, bo 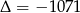Δ = − 10 71 , więc jedynym rozwiązaniem jest 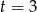t = 3 . Stąd 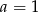a = 1 i dwa pierwsze wyrazy danego ciągu są równe

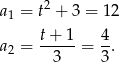
2 a1 = t + 3 = 12 t+ 1 4 a2 = ----- = -. 3 3

Iloraz ciągu jest więc równy

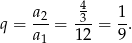
a 2 4 1 q = ---= -3-= -. a 1 12 9

Stąd wzór ciągu to

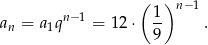
( )n −1 an = a1qn− 1 = 12 ⋅ 1- . 9

Suma wszystkich wyrazów tego ciągu geometrycznego jest równa

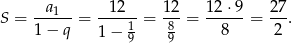
S = -a1---= --12-- = 12-= 12-⋅9-= 27. 1− q 1 − 19 89 8 2

 
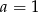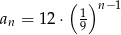Odpowiedź: a = 1 , ( 1)n− 1 an = 12 ⋅ 9 , 27 S = 2-

Wersja PDF