Zadanie nr 1086534
Wykaż, że dla każdej liczby naturalnej 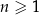 liczba
liczba 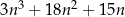 jest podzielna przez 6.
jest podzielna przez 6.
Rozwiązanie
Oczywiście
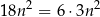
jest liczbą podzielną przez 6, więc wystarczy udowodnić, że liczba
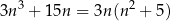
dzieli się przez 6. To z kolei sprowadza się do udowodnienia, że liczba
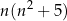
jest parzysta. Rzeczywiście tak jest, bo albo  jest liczbą parzystą, albo
jest liczbą parzystą, albo  jest liczbą nieparzystą i wtedy
jest liczbą nieparzystą i wtedy
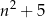
jest sumą dwóch liczb nieparzystych, czyli jest liczbą parzystą.

