/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 1912445

Dodaj do ulubionych
Dodaj do rozwiązanych

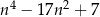Udowodnij, że jeżeli liczba całkowita n nie jest podzielna przez 3, to wyrażenie n 4 − 1 7n2 + 7 jest podzielne przez 9.

Rozwiązanie

Sposób I

Zauważmy najpierw, że

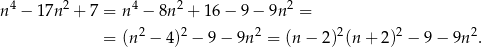
4 2 4 2 2 n − 17n + 7 = n − 8n + 16 − 9 − 9n = = (n2 − 4)2 − 9 − 9n 2 = (n − 2)2(n + 2)2 − 9 − 9n 2.

Teraz wystarczy zauważyć, że jeżeli 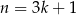n = 3k + 1 , to liczba w drugim nawiasie dzieli się przez 3, a jeżeli 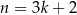n = 3k + 2 , to przez 3 podzielna jest liczba w pierwszym nawiasie. W obu przypadkach powyższe wyrażenie dzieli się przez 9.

Sposób II

Zauważmy najpierw, że

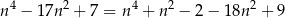
n 4 − 1 7n2 + 7 = n4 + n2 − 2 − 18n 2 + 9

oraz

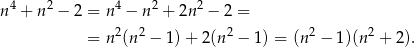
n 4 + n 2 − 2 = n4 − n2 + 2n2 − 2 = 2 2 2 2 2 = n (n − 1) + 2(n − 1) = (n − 1)(n + 2).

(Mogliśmy rozłożyć ten wielomian innymi sposobami: przez podstawienie 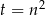t = n 2 lub szukając pierwiastków całkowitych wśród dzielników wyrazu wolnego.)

Mamy zatem

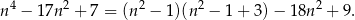
n 4 − 17n2 + 7 = (n 2 − 1)(n 2 − 1 + 3 )− 1 8n2 + 9.

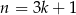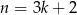Teraz wystarczy zauważyć, że jeżeli n = 3k+ 1 lub n = 3k + 2 , to liczba

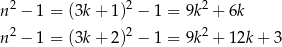
2 2 2 n − 1 = (3k + 1) − 1 = 9k + 6k n2 − 1 = (3k + 2)2 − 1 = 9k2 + 12k + 3

dzieli się przez 3. To oznacza, że dane wyrażenie dzieli się przez 9.

Wersja PDF