Zadanie nr 1924170
Wykaż, że różnica kwadratów dwóch kolejnych liczb parzystych jest liczbą podzielną przez 4.
Rozwiązanie
Sposób I
Oznaczmy dwie kolejne liczby parzyste przez 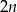 i
i 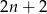 . Wtedy
. Wtedy
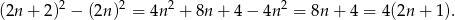
Widać, że jest to liczba podzielna przez 4.
Sposób II
Kwadrat liczby parzystej zawsze dzieli się przez cztery, więc różnica kwadratów dwóch liczb parzystych też musi dzielić się przez 4.

