Zadanie nr 2070392
Udowodnij, że dla każdej liczby całkowitej 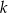 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 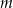 liczba
liczba 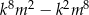 jest podzielna przez 36.
jest podzielna przez 36.
Rozwiązanie
Zauważmy, że
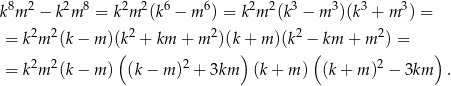
Widać teraz, że liczba ta dzieli się przez 4 – jeżeli 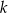 lub
lub 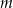 są parzyste, to przez 4 dzieli się
są parzyste, to przez 4 dzieli się 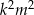 , a jeżeli obie są nieparzyste, to przez 4 dzieli się
, a jeżeli obie są nieparzyste, to przez 4 dzieli się 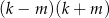 .
.
Zastanówmy się nad podzielnością przez 9. Jeżeli jedna z liczb 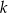 lub
lub 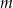 dzieli się przez 3, to podzielny przez 9 jest iloczyn
dzieli się przez 3, to podzielny przez 9 jest iloczyn 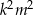 . Jeżeli liczby
. Jeżeli liczby 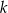 i
i 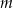 dają takie same reszty z dzielenia przez 3, to
dają takie same reszty z dzielenia przez 3, to 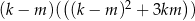 dzieli się przez 9. Podobnie, jeżeli reszty z dzielenia
dzieli się przez 9. Podobnie, jeżeli reszty z dzielenia 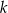 i
i 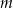 przez 3 to 1 i 2 lub 2 i 1 (w jakiejkolwiek kolejności), to przez 9 dzieli się
przez 3 to 1 i 2 lub 2 i 1 (w jakiejkolwiek kolejności), to przez 9 dzieli się 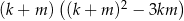 .
.
Zatem rzeczywiście liczba 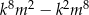 zawsze dzieli się przez
zawsze dzieli się przez 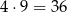 .
.

