Zadanie nr 2492443
Wykaż, że dla każdej liczby naturalnej 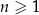 liczba
liczba 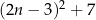 jest podzielna przez 8.
jest podzielna przez 8.
Rozwiązanie
Zauważmy, że
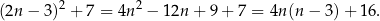
Wystarczy zatem udowodnić, że liczba
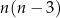
jest parzysta – a tak jest, bo zawsze albo  albo
albo 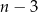 jest liczbą parzystą.
jest liczbą parzystą.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że dla każdej liczby naturalnej 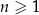 liczba
liczba 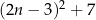 jest podzielna przez 8.
jest podzielna przez 8.
Zauważmy, że
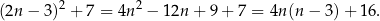
Wystarczy zatem udowodnić, że liczba
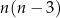
jest parzysta – a tak jest, bo zawsze albo  albo
albo 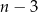 jest liczbą parzystą.
jest liczbą parzystą.
