Zadanie nr 2864942

Wykaż, że liczba 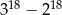18 18 3 − 2 jest podzielna przez 19.

Rozwiązanie

Sposób I

Będziemy rozkładać podane wyrażenie korzystając ze wzorów

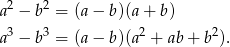
a2 − b2 = (a − b)(a + b) a3 − b3 = (a − b)(a2 + ab + b2).

Z którego z tych wzorów będziemy korzystać najpierw? Zastanówmy się co chcemy dostać. Jak się chwilkę pokombinuje, to można zauważyć, że

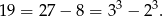
3 3 19 = 27 − 8 = 3 − 2 .

Będziemy więc przekształcać podane wyrażenie, żeby dostać 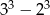3 3 3 − 2 .

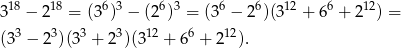
18 18 63 6 3 6 6 12 6 12 3 − 2 = (3 ) − (2 ) = (3 − 2 )(3 + 6 + 2 ) = (3 3 − 2 3)(3 3 + 23)(3 12 + 66 + 212).

No i otrzymaliśmy to co chcieliśmy, pierwszy składnik jest równy 19.

Sposób II

Korzystamy ze wzoru

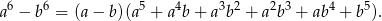
6 6 5 4 3 2 2 3 4 5 a − b = (a− b)(a + a b+ a b + a b + ab + b ).

Mamy zatem

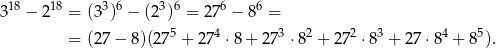
318 − 218 = (33)6 − (23)6 = 276 − 86 = = (27 − 8)(275 + 274 ⋅8 + 273 ⋅82 + 272 ⋅ 83 + 2 7⋅84 + 85).

Widać teraz, że liczba ta dzieli się przez 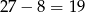27− 8 = 19 .

Sposób III

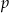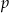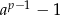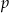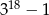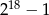Zadanie łatwo wynika z tzw. małego twierdzenia Fermata. Mówi on, że jeżeli jest liczbą pierwszą i jest względnie pierwsze z , to liczba p−1 a − 1 jest podzielna przez . Zatem 19 dzieli liczby 318 − 1 oraz 218 − 1 . Dzieli więc też ich różnicę