/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 3760846

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnych liczb całkowitych 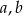a,b liczba 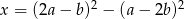2 2 x = (2a− b) − (a− 2b) jest podzielna przez 3.

Rozwiązanie

Sposób I

Zauważmy, że

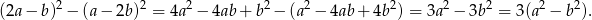
2 2 2 2 2 2 2 2 2 2 (2a− b) − (a − 2b) = 4a − 4ab + b − (a − 4ab + 4b ) = 3a − 3b = 3 (a − b ).

Widać teraz, że liczba ta rzeczywiście dzieli się przez 3.

Sposób II

Tym razem korzystamy ze wzoru na różnice kwadratów.

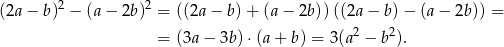
2 2 (2a − b ) − (a − 2b) = ((2a− b)+ (a − 2b ))((2a − b)− (a− 2b)) = = (3a− 3b)⋅(a + b) = 3(a2 − b2).

Widać, że otrzymana liczba dzieli się przez 3.

Wersja PDF