Zadanie nr 4217876
Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych parzystych jest podzielna przez 24.
Rozwiązanie
Trzy kolejne parzyste liczby naturalne możemy oznaczyć przez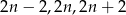 
. Zatem ich suma sześcianów jest równa
![[ ] (2n − 2)3 + (2n )3 + (2n+ 2)3 = 8 (n− 1)3 + n3 + (n + 1)3 = [ ] = 8 (n3 − 3n 2 + 3n − 1)+ n3 + (n3 + 3n2 + 3n + 1) = = 8 (3n3 + 6n) = 2 4(n3 + 2n).](https://img.zadania.info/zad/4217876/HzadR1x.gif)
Teraz widać gołym okiem, że powyższa suma jest liczbą podzielną przez 24.
