/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 5107154

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że liczba 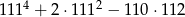4 2 111 + 2 ⋅111 − 110 ⋅112 jest dzielnikiem liczby

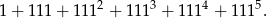
2 3 4 5 1+ 111+ 111 + 111 + 111 + 11 1 .

Rozwiązanie

Dane wyrażenie to suma kolejnych wyrazów ciągu geometrycznego o ilorazie 111, więc korzystając ze wzoru 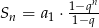n Sn = a1 ⋅ 1−1q−q na sumę kolejnych wyrazów ciągu geometrycznego mamy

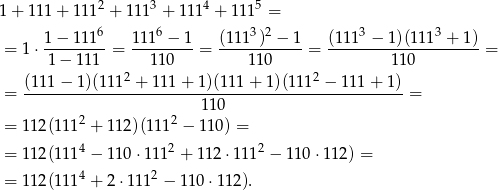
1+ 111 + 1112 + 111 3 + 11 14 + 1115 = 1-−-1116- 1116-−-1- (1113)2-−-1- (1113-−-1)(1113-+-1)- = 1 ⋅1 − 1 11 = 1 10 = 110 = 11 0 = 2 2 = (111-−-1-)(111-+--111-+-1)(111-+-1)(1-11-−--111+--1) = 11 0 = 112(1 112 + 112)(1112 − 110 ) = 4 2 2 = 112(1 11 − 110⋅ 111 + 112 ⋅111 − 110 ⋅112) = = 112(1 114 + 2⋅11 12 − 110⋅ 112).

Widać teraz gołym okiem, że otrzymana liczba dzieli się przez 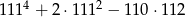11 14 + 2 ⋅111 2 − 11 0⋅1 12 .

Wersja PDF