Zadanie nr 5487875
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 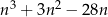 jest podzielna przez 6.
jest podzielna przez 6.
Rozwiązanie
Sposób I
Zauważmy, że
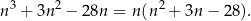
Rozłóżmy jeszcze trójmian w nawiasie.
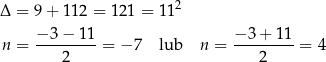
W takim razie
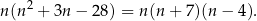
Widać teraz, że liczba ta jest parzysta – bo albo  albo
albo 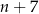 jest liczbą parzystą. Wystarczy jeszcze udowodnić, że liczba ta dzieli się przez 3. To jest oczywiste jeżeli samo
jest liczbą parzystą. Wystarczy jeszcze udowodnić, że liczba ta dzieli się przez 3. To jest oczywiste jeżeli samo  dzieli się przez 3, więc załóżmy, że
dzieli się przez 3, więc załóżmy, że  nie dzieli się przez 3. Wtedy
nie dzieli się przez 3. Wtedy 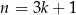 lub
lub 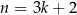 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 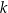 W pierwszym przypadku
W pierwszym przypadku
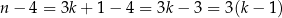
a w drugim
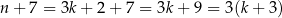
dzieli się przez 3.
Sposób II
Zauważmy najpierw, że liczba
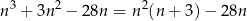
jest parzysta, bo albo  albo
albo 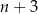 jest liczbą parzystą. Wystarczy więc udowodnić, że liczba
jest liczbą parzystą. Wystarczy więc udowodnić, że liczba
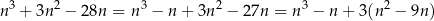
dzieli się przez 3. To z kolei sprowadza się do udowodnienia, że liczba
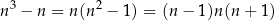
dzieli się przez 3. A to jest prawda, bo powyższe wyrażenie to iloczyn 3 kolejnych liczb całkowitych i jedna z tych 3 liczb musi dzielić się przez 3.

