/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 5776814

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że reszta z dzielenia sumy kwadratów czterech kolejnych liczb naturalnych przez 8 jest równa 6.

Rozwiązanie

Oznaczmy przez n dowolną liczbę naturalną. Wówczas czterema kolejnymi liczbami naturalnymi będą

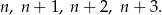
n, n+ 1, n + 2, n + 3 .

Obliczmy ile wynosi suma kwadratów tych liczb

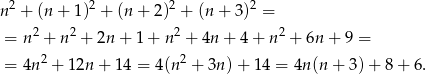
2 2 2 2 n + (n + 1) + (n + 2) + (n + 3) = = n2 + n2 + 2n + 1 + n 2 + 4n + 4+ n2 + 6n + 9 = = 4n2 + 12n + 14 = 4(n 2 + 3n )+ 14 = 4n(n + 3)+ 8 + 6 .

Zauważmy teraz, że liczba 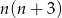n(n + 3) jest zawsze parzysta, więc liczba 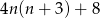4n (n+ 3)+ 8 dzieli się przez 8 i rzeczywiście interesująca nas liczba daje resztę 6 przy dzieleniu przez 8.

Wersja PDF