Zadanie nr 5910452
Udowodnij, że po wymnożeniu kolejnych liczb naturalnych od 1 do 30, czyli po wykonaniu działania 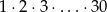 , otrzymamy liczbę, która kończy się dokładnie 7 zerami.
, otrzymamy liczbę, która kończy się dokładnie 7 zerami.
Rozwiązanie
Musimy wykazać, że dany iloczyn dzieli się przez 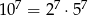 , ale nie dzieli się przez
, ale nie dzieli się przez 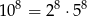 .
.
Oczywiście iloczyn ten jest podzielny przez
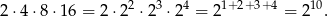
Wystarczy więc zająć się podzielnością przez 5. Wszystkie liczby podzielne przez 5 i nie większe niż 30 to
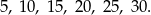
Zatem największa potęga 5-ki przez jaką dzieli się iloczyn 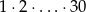 to
to
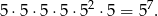
To oznacza, że rzeczywiście liczba 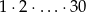 dzieli się przez
dzieli się przez 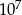 , ale nie dzieli się przez
, ale nie dzieli się przez 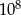 .
.

