/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 7748927

Dodaj do ulubionych
Dodaj do rozwiązanych

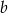Reszta z dzielenia liczby naturalnej a przez 6 jest równa 1. Reszta z dzielenia liczby naturalnej b przez 6 jest równa 5. Uzasadnij, że liczba 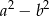a2 − b2 jest podzielna przez 24.

Rozwiązanie

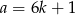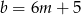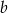Z podanych informacji wiemy, że a = 6k+ 1 i b = 6m + 5 dla pewnych liczb całkowitych a i b . Mamy więc

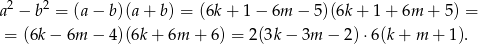
2 2 a − b = (a − b)(a + b) = (6k + 1 − 6m − 5)(6k + 1 + 6m + 5) = = (6k − 6m − 4)(6k + 6m + 6) = 2 (3k− 3m − 2) ⋅6(k + m + 1).

Z powyższego rozkładu jest jasne, że otrzymana liczba dzieli się przez 12. Aby udowodnić, że liczba ta dzieli przez 24 trzeba uzasadnić, że jedna z liczb w nawiasach jest parzysta.

Sposób I

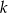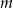Jeżeli k i m są tej samej parzystości, to liczba

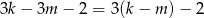
3k − 3m − 2 = 3(k − m )− 2

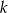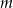jest parzysta, a jeżeli k i m są różnej parzystości, to parzysta jest liczba k + m + 1 .

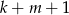Sposób II

Zauważmy, że

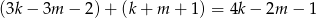
(3k − 3m − 2) + (k+ m + 1 ) = 4k− 2m − 1

jest liczbą nieparzystą, więc liczby w nawiasach są różnej parzystości. Jedna z nich jest więc parzysta.

Wersja PDF