/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 7969738

Dodaj do ulubionych
Dodaj do rozwiązanych

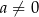Wyznacz wszystkie liczby całkowite a , gdzie a ⁄= 0 , dla których liczba 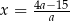x = 4a−a15 jest liczbą naturalną.

Rozwiązanie

Przekształćmy dany ułamek tak, aby pozbyć się a z licznika.

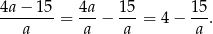
4a − 1 5 4a 15 15 -------- = ---− ---= 4− --. a a a a

Widać teraz, że liczba ta będzie całkowita tylko wtedy, gdy liczba a jest dzielnikiem 15, czyli jedną z liczb

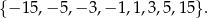
{− 15,− 5,− 3,− 1,1,3,5,15 }.

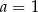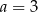Musimy jednak uważać, bo dany ułamek ma być liczbą naturalną, czyli musi być dodatni. To eliminuje wartości a = 1 i a = 3 . Mamy zatem

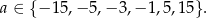
a ∈ {− 15,− 5,− 3,− 1,5,15} .

 
Odpowiedź: a ∈ {− 15 ,−5 ,−3 ,−1 ,5,15}

Wersja PDF