/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 9846060

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że jeżeli liczba całkowita nie dzieli się przez 3, to jej kwadrat przy dzieleniu przez 3 daje resztę 1.

Rozwiązanie

Sposób I

Jeżeli liczba całkowita nie dzieli się przez 3, to jest postaci 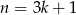n = 3k + 1 lub n = 3k+ 2 .

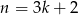W pierwszym przypadku kwadrat tej liczby jest równy

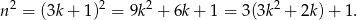
n2 = (3k + 1)2 = 9k2 + 6k + 1 = 3(3k2 + 2k)+ 1.

Widać teraz, że rzeczywiście 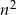n2 daje resztę 1 z dzielenia przez 3.

W drugim przypadku

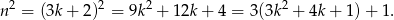
2 2 2 2 n = (3k + 2 ) = 9k + 12k + 4 = 3(3k + 4k + 1) + 1.

Zatem tak jak poprzednio 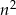2 n daje resztę 1 z dzielenia przez 3.

Sposób II

Zauważmy, że wystarczy wykazać, że liczba

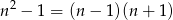
n2 − 1 = (n − 1)(n+ 1)

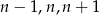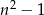jest podzielna przez 3. Wśród trzech kolejnych liczb całkowitych: n − 1 ,n ,n + 1 jest jedna podzielna przez 3. Z założenia wiemy, że n nie dzieli się przez 3, więc jedna z dwóch pozostałych liczb musi dzielić się przez 3. To dowodzi, że n2 − 1 rzeczywiście jest liczbą podzielną przez 3.

Wersja PDF