/Szkoła średnia/Liczby/Liczby całkowite

Zadanie nr 9852856

Dodaj do ulubionych
Dodaj do rozwiązanych

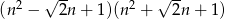Uzasadnij, że jeżeli n jest liczbą całkowitą to liczba 2 √ -- 2 √ -- (n − 2n + 1)(n + 2n + 1 ) też jest liczbą całkowitą.

Rozwiązanie

Wymnożymy podane wyrażenie. Można to zrobić ’na siłę’, ale można też zauważyć, że mamy do czynienia ze wzorem na różnicę kwadratów.

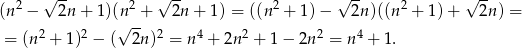
2 √ -- 2 √ -- 2 √ -- 2 √ -- (n − 2n + 1)(n + 2n + 1) = ((n + 1 )− 2n )((n + 1)+ 2n) = 2 2 √ -- 2 4 2 2 4 = (n + 1 ) − ( 2n ) = n + 2n + 1 − 2n = n + 1.

Teraz jest jasne, że liczba ta jest liczbą całkowitą.

Wersja PDF