Zadanie nr 2139227
Sinusy kątów ostrych trójkąta prostokątnego oraz liczba 1 tworzą ze sobą ciąg geometryczny. Oblicz sinus najmniejszego kąta tego trójkąta.
Rozwiązanie
Jeżeli 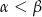 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 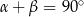 .
.

Zatem
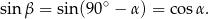
Wiemy więc, że liczby o których mowa, to 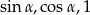 . Musimy jeszcze ustalić w jakiej kolejności tworzą one ciąg geometryczny. Na pewno jedynka to największy z wyrazów (bo
. Musimy jeszcze ustalić w jakiej kolejności tworzą one ciąg geometryczny. Na pewno jedynka to największy z wyrazów (bo 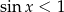 dla kąta ostrego
dla kąta ostrego  ). Ponadto sinus jest funkcją rosnącą dla kątów ostrych, więc z naszego założenia
). Ponadto sinus jest funkcją rosnącą dla kątów ostrych, więc z naszego założenia 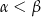 mamy
mamy
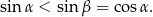
Zatem ciąg geometryczny, o którym mowa w treści zadania, to 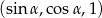 . W ciągu geometrycznym kwadrat każdego wyrazu jest iloczynem wyrazów sąsiednich, więc mamy równanie
. W ciągu geometrycznym kwadrat każdego wyrazu jest iloczynem wyrazów sąsiednich, więc mamy równanie
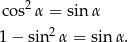
Podstawiamy teraz 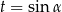
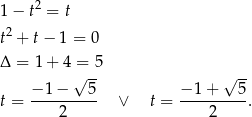
Pierwiastek ujemny odrzucamy (bo kąt  jest ostry) i mamy
jest ostry) i mamy 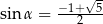 .
.
Odpowiedź: