/Szkoła średnia/Ciągi/Geometryczny/W geometrii

Zadanie nr 2483788

Długości boków trójkąta 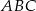ABC są kolejnymi wyrazami ciągu geometrycznego o ilorazie 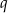q . Wykaż, że miary kątów trójkąta zbudowanego z odcinków o długościach równych długościom wysokości trójkąta 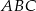ABC są równe miarom kątów trójkąta ABC .

Wersja PDF

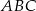Rozwiązanie

Dwa trójkąty mają równe kąty dokładnie wtedy, gdy są podobne. Musimy więc wykazać podobieństwo dwóch opisanych trójkątów.

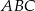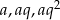Oznaczmy boki trójkąta ABC przez a,aq,aq 2 , a opuszczone na te boki wysokości przez 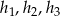h ,h ,h 1 2 3 . W takim razie, ze wzoru na pole 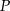P trójkąta mamy

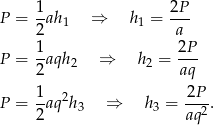
1 2P P = --ah1 ⇒ h1 = --- 2 a P = 1-aqh2 ⇒ h2 = 2P- 2 aq 1 2 2P P = --aq h3 ⇒ h3 = --2. 2 aq

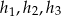Zauważmy, że ponownie otrzymaliśmy wyrazy ciągu geometrycznego, ale o ilorazie 1q . To oznacza, że trójkąt o bokach h1,h2,h 3 jest podobny do wyjściowego trójkąta, a dokładniej

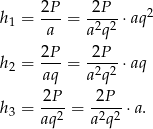
2P- -2P-- 2 h 1 = a = a2q2 ⋅aq h 2 = 2P- = -2P--⋅aq aq a2q2 2P 2P h 3 = --2-= -2-2-⋅a. aq a q

Trójkąty są więc podobne w skali 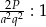-2P- a2q2 : 1 , czyli mają równe kąty.

Wersja PDF