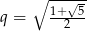Zadanie nr 8635341
Długości boków trójkąta prostokątnego są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego. Oblicz iloraz tego ciągu.
Rozwiązanie
Sposób I
Oznaczmy boki trójkąta przez 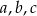 . Ponieważ będziemy chcieli napisać warunek, że są to kolejne wyrazy rosnącego ciągu geometrycznego, to ustalmy ich kolejność, tzn. załóżmy, że
. Ponieważ będziemy chcieli napisać warunek, że są to kolejne wyrazy rosnącego ciągu geometrycznego, to ustalmy ich kolejność, tzn. załóżmy, że 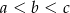 . Mamy zatem dwa równania
. Mamy zatem dwa równania
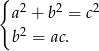
Pierwsze z nich to twierdzenie Pitagorasa, drugie to podstawowa własność ciągu geometrycznego. W pierwszej chwili można się przestraszyć, bo niewiadome są trzy a równania tylko dwa. Ale my nie chcemy wyliczyć 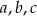 (zresztą nie da się tego zrobić) tylko iloraz dwóch kolejnych, a to duża różnica. Mając to na uwadze, podstawmy do pierwszego równania
(zresztą nie da się tego zrobić) tylko iloraz dwóch kolejnych, a to duża różnica. Mając to na uwadze, podstawmy do pierwszego równania 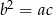 i przekształćmy otrzymane równanie żeby wyliczyć
i przekształćmy otrzymane równanie żeby wyliczyć  .
.
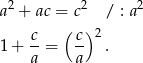
Podstawiamy teraz 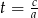 i dostajemy równanie kwadratowe
i dostajemy równanie kwadratowe 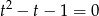 , które ma pierwiastki
, które ma pierwiastki 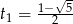 i
i 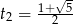 . Bierzemy drugi, bo ciąg ma być rosnący. Zatem
. Bierzemy drugi, bo ciąg ma być rosnący. Zatem
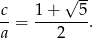
Czy to jest szukany iloraz? Niezupełnie, wpadliśmy w pułapkę, którą sami na siebie zastawiliśmy,  i
i  to nie są kolejne wyrazy ciągu geometrycznego, tylko wyrazy
to nie są kolejne wyrazy ciągu geometrycznego, tylko wyrazy 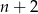 i
i  , czyli coś w stylu
, czyli coś w stylu 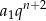 i
i 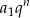 . W takim razie, to co wyliczyliśmy to jest
. W takim razie, to co wyliczyliśmy to jest 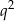 , a
, a 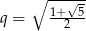 .
.
Sposób II
Załóżmy, że ciąg geometryczny z treści zadania ma postać 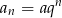 ,
, 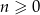 i niech
i niech 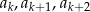 będą długościami boków trójkąta prostokątnego dla pewnego
będą długościami boków trójkąta prostokątnego dla pewnego 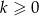 . Z twierdzenia Pitagorasa
. Z twierdzenia Pitagorasa
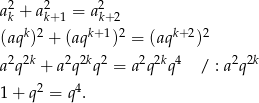
Otrzymane równanie dwukwadratowe rozwiązujemy standardowo podstawiając 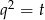 . Tak jak w poprzednim sposobie, otrzymujemy
. Tak jak w poprzednim sposobie, otrzymujemy
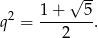
Odpowiedź: