/Szkoła średnia/Ciągi/Geometryczny/W geometrii

Zadanie nr 8805151

Dodaj do ulubionych
Dodaj do rozwiązanych

Długości trzech krawędzi prostopadłościanu tworzą ciąg geometryczny. Objętość bryły jest równa 27, a suma długości jej krawędzi jest równa 52. Znajdź długość najkrótszej krawędzi prostopadłościanu.

Rozwiązanie

Zaczynamy od rysunku

PIC

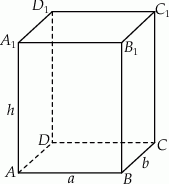
Możemy założyć, że krawędzie tworzą ciąg geometryczny w następującej kolejności 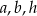a,b,h . Zatem

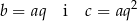
b = aq i c = aq 2

Wykorzystujemy informację o objętości

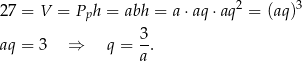
27 = V = Pph = abh = a⋅ aq⋅aq 2 = (aq)3 3 aq = 3 ⇒ q = --. a

Wykorzystujemy drugą informację

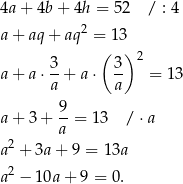
4a + 4b + 4h = 52 / : 4 a + aq + aq2 = 13 ( ) 2 a + a ⋅ 3-+ a ⋅ 3- = 13 a a 9 a + 3 + --= 13 /⋅ a a a2 + 3a + 9 = 13a 2 a − 10a + 9 = 0.

Obliczamy wyznacznik i pierwiastki

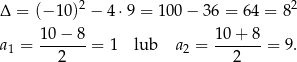
2 2 Δ = (− 10) − 4 ⋅9 = 10 0− 3 6 = 64 = 8 10-−-8- 10-+-8- a 1 = 2 = 1 lub a2 = 2 = 9.

Zatem

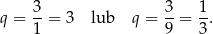
q = 3-= 3 lub q = 3-= 1. 1 9 3

Jeżeli policzymy pozostałe długości krawędzi to zauważymy, że w obu przypadkach dadzą te same wartości (tylko w różnej kolejności). Zatem krawędzie mają długość

1,3,9.

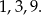
Czyli najkrótsza krawędź ma długość 1.  
Odpowiedź: 1

Wersja PDF