/Szkoła średnia/Ciągi/Geometryczny/W geometrii

Zadanie nr 9740679

Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?

Wersja PDF

Rozwiązanie

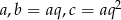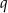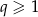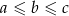Niech 2 a,b = aq,c = aq będą długościami boków trójkąta, które tworzą ciąg geometryczny o ilorazie q . Jeżeli założymy, że q ≥ 1 , to a ≤ b ≤ c i na mocy nierówności trójkąta, taki trójkąt istnieje wtedy i tylko wtedy gdy

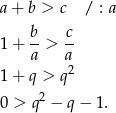
a + b > c / : a 1 + b-> c- a a 1 + q > q2 2 0 > q − q − 1.

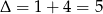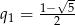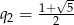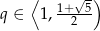Dalej, Δ = 1 + 4 = 5 , √ - q1 = 1−2-5 , √ - q2 = 1+2-5 . Zatem ⟨ √ -) q ∈ 1, 1+2-5 .

Jeżeli natomiast 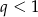q < 1 , to możemy zastosować powyższe rozumowanie do boków 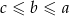c ≤ b ≤ a , które tworzą ciąg geometryczny o ilorazie 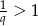1 q > 1 . Mamy wtedy

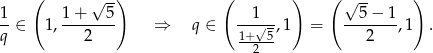
( √ -) ( ) ( √ -- ) 1- 1-+---5- --1--- --5-−-1- q ∈ 1, 2 ⇒ q ∈ 1+√-5,1 = 2 ,1 . 2

 
Odpowiedź: ( √- √ -) -5−-1 1+--5 q ∈ 2 , 2

Wersja PDF