/Szkoła średnia/Ciągi/Szereg geometryczny/Badanie zbieżności

Zadanie nr 1755280

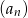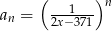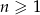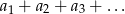Dany jest ciąg geometryczny (an) określony wzorem ( 1 )n an = 2x−-371 dla n ≥ 1 . Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą x , dla której nieskończony szereg a + a + a + ... 1 2 3 jest zbieżny.

Wersja PDF

Rozwiązanie

Informacje o tym, że ciąg jest zbieżny oraz, że ma wyrazy dodatnie możemy zapisać przy pomocy nierówności

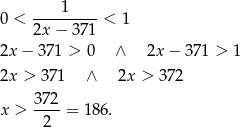
0 < ----1---- < 1 2x − 371 2x − 371 > 0 ∧ 2x− 371 > 1 2x > 371 ∧ 2x > 372 372- x > 2 = 186.

Najmniejsza liczba całkowita spełniająca tę nierówność to 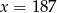x = 187 .  
Odpowiedź: x = 187

Wersja PDF