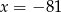/Szkoła średnia/Ciągi/Szereg geometryczny/Badanie zbieżności

Zadanie nr 8301859

Dodaj do ulubionych
Dodaj do rozwiązanych

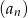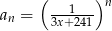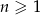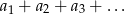Dany jest ciąg geometryczny (an) określony wzorem ( 1 )n an = 3x+-241 dla n ≥ 1 , którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą x , dla której nieskończony szereg a + a + a + ... 1 2 3 jest zbieżny.

Rozwiązanie

Oczywiście mamy do czynienia z ciągiem geometrycznym o ilorazie 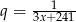q = 3x1+241 . Wiemy, że niektóre wyrazy są ujemne, więc 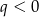q < 0 . W takim razie szereg 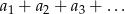a1 + a2 + a3 + ... jest zbieżny jeżeli 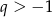q > − 1 . Musimy więc rozwiązać nierówność

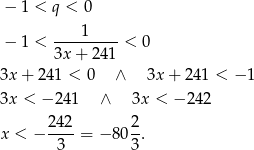
− 1 < q < 0 1 − 1 < ---------< 0 3x + 241 3x+ 241 < 0 ∧ 3x+ 241 < − 1 3x < − 241 ∧ 3x < − 242 242- 2- x < − 3 = − 803 .

 
Odpowiedź: x = −8 1

Wersja PDF