Zadanie nr 2978239
Wyrazy 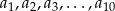 pewnego nieskończonego ciągu
pewnego nieskończonego ciągu 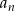 spełniają warunki
spełniają warunki 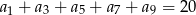 ,
, 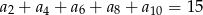 . Wiedząc, że nieskończony ciąg
. Wiedząc, że nieskończony ciąg 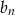 określony wzorem
określony wzorem 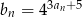 jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu
jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu 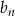 .
.
Rozwiązanie
Sprawdźmy kiedy ciąg 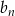 jest ciągiem geometrycznym – iloraz jego sąsiednich wyrazów musi być stały.
jest ciągiem geometrycznym – iloraz jego sąsiednich wyrazów musi być stały.
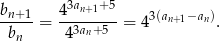
Aby wyrażenie to nie zależało od  , to samo musi być prawdą dla różnicy
, to samo musi być prawdą dla różnicy 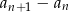 , zatem ciąg
, zatem ciąg 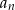 musi być ciągiem arytmetycznym.
musi być ciągiem arytmetycznym.
Aby zapisać podane równości zauważmy, że jeżeli  jest różnicą ciągu
jest różnicą ciągu 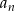 , to ciągi
, to ciągi 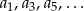 i
i 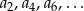 są ciągami arytmetycznymi o różnicy
są ciągami arytmetycznymi o różnicy 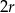 . Zatem podane warunki dają nam równania.
. Zatem podane warunki dają nam równania.
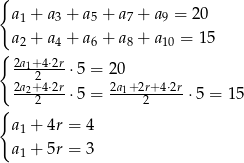
Odejmując od drugiego równania pierwsze (żeby skrócić 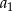 ) mamy
) mamy 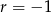 , czyli
, czyli 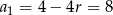 oraz
oraz
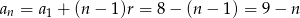
Daje nam to
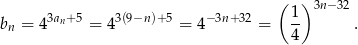
Widać, że ciąg 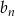 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 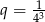 . Jego suma wynosi więc
. Jego suma wynosi więc
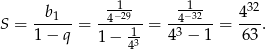
Odpowiedź: