Zadanie nr 4577356
Określamy kwadraty 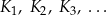 następująco:
następująco:
-
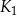 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
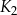 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 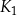 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2 -
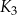 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 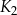 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2
i ogólnie, dla każdej liczby naturalnej 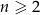 ,
,
-
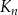 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 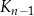 i dzieli ten bok w stosunku 1 : 2.
i dzieli ten bok w stosunku 1 : 2.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
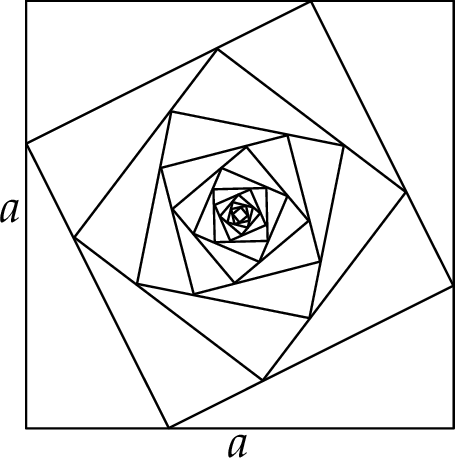
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

